Monday, January 13, 2014

Simple harmonic motion

                No comments   

Simple harmonic motion

Simple harmonic oscillator

Main article: Simple harmonic motion

Simple harmonic motion
A simple harmonic oscillator is an oscillator that is neither driven nor damped. It consists of a mass m, which experiences a single force, F, which pulls the mass in the direction of the point x=0 and depends only on the mass's position x and a constant k. Balance of forces (Newton's second law) for the system is

F = m a = m \frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -k x.
Solving this differential equation, we find that the motion is described by the function
x(t) = A\cos\left( \omega t+\phi\right),
where
\omega = \sqrt{\frac{k}{m}} = \frac{2\pi}{T}.
The motion is periodic, repeating itself in a sinusoidal fashion with constant amplitude, A. In addition to its amplitude, the motion of a simple harmonic oscillator is characterized by its period T, the time for a single oscillation or its frequency f = 1⁄T, the number of cycles per unit time. The position at a given time t also depends on the phase, φ, which determines the starting point on the sine wave. The period and frequency are determined by the size of the mass m and the force constant k, while the amplitude and phase are determined by the starting position and velocity.
The velocity and acceleration of a simple harmonic oscillator oscillate with the same frequency as the position but with shifted phases. The velocity is maximum for zero displacement, while the acceleration is in the opposite direction as the displacement.
The potential energy stored in a simple harmonic oscillator at position x is

 

From Wikipedia, the free encyclopedia
Jump to: navigation, search
In mechanics and physics, simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement. It can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. In addition, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum as well as molecular vibration. Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. In order for simple harmonic motion to take place, the net force of the object at the end of the pendulum must be proportional to the displacement.
Simple harmonic motion provides a basis for the characterization of more complicated motions through the techniques of Fourier analysis.

Introduction


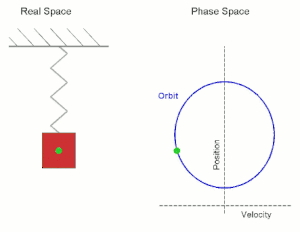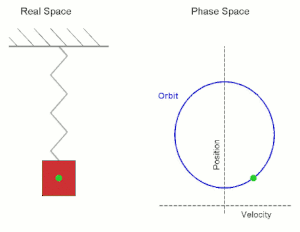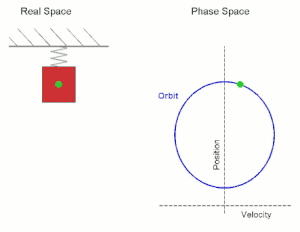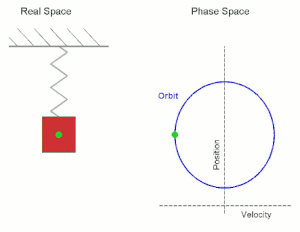
Simple harmonic motion shown both in real space and phase space. The orbit is periodic. (Here the velocity and position axes have been reversed from the standard convention in order to align the two diagrams)
In the diagram a simple harmonic oscillator, comprising a mass attached to one end of a spring, is shown. The other end of the spring is connected to a rigid support such as a wall. If the system is left at rest at the equilibrium position then there is no net force acting on the mass. However, if the mass is displaced from the equilibrium position, a restoring elastic force which obeys Hooke's law is exerted by the spring.
Mathematically, the restoring force F is given by
\mathbf{F}=-k\mathbf{x},
where F is the restoring elastic force exerted by the spring (in SI units: N), k is the spring constant (N·m−1), and x is the displacement from the equilibrium position (in m).
For any simple harmonic oscillator:
  • When the system is displaced from its equilibrium position, a restoring force which resembles Hooke's law tends to restore the system to equilibrium.
Once the mass is displaced from its equilibrium position, it experiences a net restoring force. As a result, it accelerates and starts going back to the equilibrium position. When the mass moves closer to the equilibrium position, the restoring force decreases. At the equilibrium position, the net restoring force vanishes. However, at x = 0, the mass has momentum because of the impulse that the restoring force has imparted. Therefore, the mass continues past the equilibrium position, compressing the spring. A net restoring force then tends to slow it down, until its velocity reaches zero, whereby it will attempt to reach equilibrium position again.
As long as the system has no energy loss, the mass will continue to oscillate. Thus, simple harmonic motion is a type of periodic motion.

Dynamics of simple harmonic motion

For one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, could be obtained by means of Newton's second law and Hooke's law.
F_{net} = m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -kx,
where m is the inertial mass of the oscillating body, x is its displacement from the equilibrium (or mean) position, and k is the spring constant.
Therefore,
\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -\left(\frac{k}{m}\right)x,
Solving the differential equation above, a solution which is a sinusoidal function is obtained.
x(t) = c_1\cos\left(\omega t\right) + c_2\sin\left(\omega t\right) = A\cos\left(\omega t - \varphi\right),
where
\omega = \sqrt{\frac{k}{m}},
A = \sqrt{{c_1}^2 + {c_2}^2},
\tan \varphi = \left(\frac{c_2}{c_1}\right),
In the solution, c1 and c2 are two constants determined by the initial conditions, and the origin is set to be the equilibrium position.[A] Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2πf is the angular frequency, and φ is the phase.[B]
Using the techniques of differential calculus, the velocity and acceleration as a function of time can be found:
v(t) = \frac{\mathrm{d} x}{\mathrm{d} t} = - A\omega \sin(\omega t+\varphi),
a(t) = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = - A \omega^2 \cos( \omega t+\varphi).
Acceleration can also be expressed as a function of displacement:
a(x) = -\omega^2 x.\!
Then since ω = 2πf,
f = \frac{1}{2\pi}\sqrt{\frac{k}{m}},
and since T = 1/f where T is the time period,
T = 2\pi \sqrt{\frac{m}{k}}.
These equations demonstrate that the simple harmonic motion is isochronous (the period and frequency are independent of the amplitude and the initial phase of the motion).

Energy of simple harmonic motion

The kinetic energy K of the system at time t is
K(t) = \frac{1}{2} mv^2(t) = \frac{1}{2}m\omega^2A^2\sin^2(\omega t - \varphi) = \frac{1}{2}kA^2 \sin^2(\omega t - \varphi),
and the potential energy is
U(t) = \frac{1}{2} k x^2(t) = \frac{1}{2} k A^2 \cos^2(\omega t - \varphi).
The total mechanical energy of the system therefore has the constant value
E = K + U = \frac{1}{2} k A^2.

Examples


An undamped spring–mass system undergoes simple harmonic motion.
The following physical systems are some examples of simple harmonic oscillator.

Mass on a spring

A mass m attached to a spring of spring constant k exhibits simple harmonic motion in closed space. The equation
T= 2 \pi{\sqrt{\frac{m}{k}}}
shows that the period of oscillation is independent of both the amplitude and gravitational acceleration

Uniform circular motion

Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular speed ω around a circle of radius r centered at the origin of the x-y plane, then its motion along each coordinate is simple harmonic motion with amplitude r and angular frequency ω.

Mass on a simple pendulum


The motion of an undamped Pendulum approximates to simple harmonic motion if the amplitude is very small relative to the length of the rod.
In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The period of a mass attached to a pendulum of length ℓ with gravitational acceleration g is given by
T = 2 \pi \sqrt{\frac{\ell}{g}}
This shows that the period of oscillation is independent of the amplitude and mass of the pendulum but not the acceleration due to gravity (g), therefore a pendulum of the same length on the Moon would swing more slowly due to the Moon's lower gravitational field strength.
This approximation is accurate only in small angles because of the expression for angular acceleration α being proportional to the sine of position:
m g \ell \sin(\theta)=I \alpha,
where I is the moment of inertia. When θ is small, sin θ ≈ θ and therefore the expression becomes
-m g \ell \theta=I \alpha
which makes angular acceleration directly proportional to θ, satisfying the definition of simple harmonic motion.




ComplexSinInATimeAxe


ComplexSinInATimeAxe.gif ‎(550 × 400 pixels, file size: 201 KB, MIME type: image/gif, looped, 49 frames, 7.8 s)

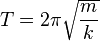
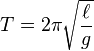
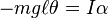
0 comments:

Post a Comment